Wykrywanie za pomocą prawa Benforda zniekształceń spowodowanych potencjalnym oszustwem
Przedmiotem badania sprawozdania finansowego (sf), obok informacji opisowych (jakościowych), są zapisy ksiąg rachunkowych (zbiory danych liczbowych). Badanie polega zwykle na wykonaniu czynności rewizyjnych, głównie wyrywkowo, odpowiednich do przedmiotu i racjonalnie poczynionych szacunków ryzyka badania, a to z uwagi na fakt, że badanie pełne na ogół nie jest celowe ze względu na czaso- i kosztochłonność.
Przedmiotem badania sprawozdania finansowego (sf), obok informacji opisowych (jakościowych), są zapisy ksiąg rachunkowych (zbiory danych liczbowych). Badanie polega zwykle na wykonaniu czynności rewizyjnych, głównie wyrywkowo, odpowiednich do przedmiotu i racjonalnie poczynionych szacunków ryzyka badania, a to z uwagi na fakt, że badanie pełne na ogół nie jest celowe ze względu na czaso- i kosztochłonność.
Badanie wyrywkowe polega na sprawdzeniu i analizie informacji/danych wybranych ze zbioru (próbka) potencjalnie obarczonego ryzykiem istotnych zniekształceń, ujemnie rzutujących na jakość sf, a następnie odniesieniu wyników badania na cały zbiór (ekstrapolacja). Może być ukierunkowane na badanie zbiorów danych przez identyfikację dowodów księgowych (np. faktur w zbiorze faktur sprzedaży), które mogą wskazywać na potencjalne „zaburzenia” tych zbiorów. W szczególności można stosunkowo prosto ustalić:
1. Czy w badanym zbiorze dublują się numery faktur?
2. Czy występują luki w kolejności numeracji faktur?
3. Czy zbiór obejmuje dokumenty, których data nie należy do okresu rozliczeniowego objętego badaniem?
4. Jaki jest rozkład faktur w zbiorze według ich kwoty (celem ustalenia, które faktury wykazują kwoty znacznie odbiegające od wartości średniej)?
5. Jaki jest rozkład faktur w zbiorze według dat ich wystawienia (celem ustalenia okresów, w których nastąpiło natężenie ich wystawiania)?
Badanie takie można przeprowadzić, korzystając z programu Excel. Wykorzystanie do badania narzędzi IT jest szczególnie wskazane, gdy biegły rewident ma zbadać zbiory złożone z wielu pozycji, np. kilkuset lub kilku tysięcy. Przy tak dużych zbiorach racjonalne jest oparcie się na mechanizmach kontroli wewnętrznej zastosowanych przez jednostkę w tym obszarze, aczkolwiek – aby tak postąpić – należy uprzednio zbadać, czy kontroli tej można zaufać.
Wymogi KSB
Obowiązek zapobiegania oszustwom i błędom oraz ich wykrywania spoczywa głównie na osobach sprawujących nadzór nad jednostką oraz na kierowniku jednostki, której sf jest przedmiotem badania. To kierownik jednostki ma obowiązek wdrożyć i zastosować odpowiednie systemy rachunkowości oraz kontroli wewnętrznej, pozwalające ograniczyć możliwość dokonywania oszustw i występowania błędów.
KSB 200 w brzmieniu MSB 200 Ogólne cele niezależnego biegłego rewidenta oraz przeprowadzanie badania zgodnie z Międzynarodowymi Standardami Badania wyjaśnia: celem badania jest zwiększenie poziomu zaufania zamierzonych użytkowników do sf. Osiąga się to dzięki wyrażeniu przez biegłego rewidenta opinii o tym, czy sf zostało, we wszystkich istotnych aspektach, sporządzone zgodnie z mającymi zastosowanie ramowymi założeniami sprawozdawczości finansowej. Samo zaś sf poddane badaniu jest sprawozdaniem jednostki sporządzonym przez kierownika jednostki pod nadzorem osób sprawujących nadzór. (…) Zbadanie sf nie zwalnia kierownika jednostki ani osób sprawujących nadzór z ich odpowiedzialności.
Opinia biegłego rewidenta o wiarygodności obrazu sytuacji i działalności badanej jednostki przekazywanego w jej sf powinna, w myśl MSB 200, wynikać z uzyskania przez niego racjonalnej pewności, że sf jako całość nie zawiera istotnego zniekształcenia. Racjonalna pewność oznacza wysoki poziom pewności, którą uzyskuje się, gdy biegły zgromadził odpowiednie i wystarczające dowody badania, obniżające ryzyko badania (tj. ryzyko wyrażenia niewłaściwej opinii przez biegłego rewidenta, w przypadku gdy sf zawiera istotne zniekształcenia) do możliwego do zaakceptowania niskiego poziomu.
Racjonalna pewność nie jest równoznaczna z absolutną pewnością, ponieważ istnieją nieuniknione ograniczenia badania spowodowane tym, że większość dowodów badania, na podstawie których biegły wyciąga wnioski i które są podstawą opinii, ma raczej charakter uprawdopodabniający niż rozstrzygający.
Zniekształcenia, o których mowa, mogą być spowodowane błędem lub oszustwem. Wymóg rozpoznania i stwierdzenia wpływu ew. nadużyć na sf stawia przed biegłym rewidentem KSB w brzmieniu MSB 240 Obowiązki biegłego rewidenta podczas badania sprawozdania finansowego dotyczące oszustw. Wskazuje on, że w ramach procedur oceny ryzyka istotnego zniekształcenia sf biegły rewident powinien również przeprowadzić procedury służące uzyskaniu informacji pozwalających na identyfikację ryzyka zniekształcenia sf spowodowanego oszustwem. Procedury te obejmują np. ocenę pozyskanych od kierownictwa lub innych osób informacji nt. stosowanego w jednostce sposobu rozpoznawania ryzyka oszustwa i reagowania na nie. Biegły rewident ocenia również, czy zidentyfikowane nietypowe bądź nieoczekiwane powiązania, które zostały rozpoznane w trakcie przeprowadzania procedur analitycznych, w tym odnoszących się do przychodów, mogą wskazywać na istotne zniekształcenie spowodowane oszustwem.
MSB 240 definiuje pojęcie „oszustwa” jako zamierzone działanie podjęte przez jednego lub kilku członków kierownictwa, osoby sprawujące nadzór, pracowników lub strony trzecie, przy wykorzystaniu kłamstwa, w celu uzyskania nieuzasadnionej lub niezgodnej z prawem korzyści. Oszustwo może polegać m.in. na manipulowaniu, fałszowaniu bądź na zmianach w ewidencji lub w dokumentach, zatuszowaniu bądź pominięciu w ewidencji i dokumentach informacji o skutkach transakcji, rejestrowaniu transakcji, do których nie doszło.
Biegły rewident, który rozpoznał zniekształcenie wskazujące na oszustwo, ocenia wpływ zniekształcenia w powiązaniu z innymi aspektami badania, a szczególnie na wiarygodność oświadczeń kierownika jednostki. W takich przypadkach biegły – przykładowo – ocenia ponownie ryzyko i ważność tych oświadczeń wobec faktu niewykrycia oszustw i błędów przez kontrolę wewnętrzną i niezawarcia odpowiedniej informacji w oświadczeniach zarządu.
W razie zidentyfikowania zniekształcenia wskazującego na popełnienie oszustwa biegły rewident określa tzw. ogólną reakcję na oszacowanie tego ryzyka na poziomie sf oraz stwierdzeń. W konsekwencji, zgodnie z KSB 330 w brzmieniu MSB 330 Reakcje biegłego rewidenta na oszacowane ryzyka, projektuje i przeprowadza dalsze procedury badania, uwzględniając ich rodzaj, rozłożenie w czasie i zakres.
Jeśli biegły rewident stwierdził fakty wskazujące na oszustwo lub będzie podejrzewał jego popełnienie, powinien niezwłocznie zawiadomić o tym kierownictwo odpowiedniego szczebla jednostki. Jeżeli natomiast stwierdził bądź podejrzewa oszustwo z udziałem kierownictwa jednostki, informuje o tym niezwłocznie osoby sprawujące nad nią nadzór.
W przypadku stwierdzenia oszustwa przez biegłego rewidenta konieczne może się okazać poinformowanie organów regulacyjnych i ścigania. MSB 240 wskazuje następujący sposób postępowania: Jeżeli biegły rewident zidentyfikował lub podejrzewa oszustwo, określa, czy spoczywa na nim obowiązek przekazania informacji o stwierdzonym lub podejrzewanym oszustwie stronom spoza jednostki. Pomimo że spoczywający na biegłym rewidencie zawodowy obowiązek zachowania poufności nt. klienta może wykluczać przekazywanie tego rodzaju informacji, (…) niemniej spoczywająca na biegłym rewidencie prawna odpowiedzialność może uchylić w pewnych okolicznościach obowiązek zachowania poufności.
Dla realizacji wymogów MSB 240 interesujące i przydatne mogą się okazać techniki badania wykorzystujące prawo Benforda, gdyż pozwalają wyselekcjonować dowody księgowe, których poprawność budzi wątpliwości.
Prawo Benforda – wprowadzenie
[1] W dalszej części artykułu pojęcia te będą stosowane wymiennie jako równoważne.
[2] Uściślając, w sposób logarytmiczny: prawdopodobieństwo wystąpienia cyfry k to Pk = log10 (k + 1 / k).
Prawo Benforda, rozkład Benforda, prawo pierwszych (znaczących) cyfr[1] to prawdopodobieństwo występowania określonej cyfry na pierwszym miejscu w rzeczywistych danych liczbowych. Rozkład wskazuje, że częstość występowania na pierwszym miejscu, w rzeczywistych danych liczbowych, kolejnych cyfr, poczynając od 1, maleje w znaczący sposób[2]. Obrazuje to poniższy rysunek.
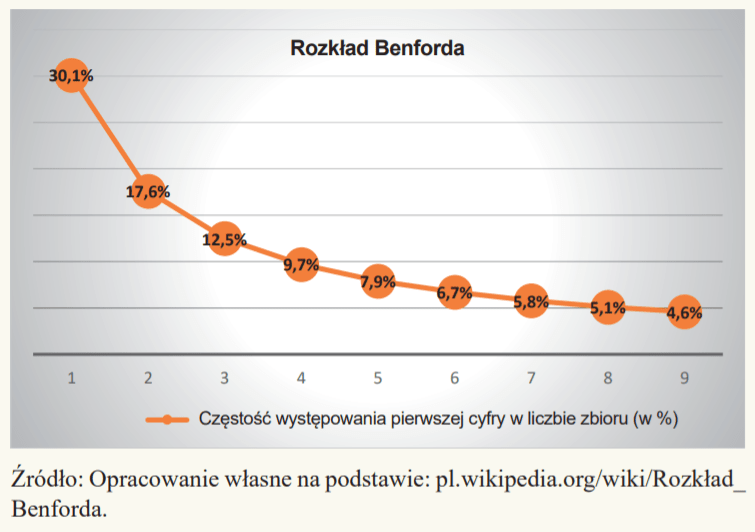
Charakterystyczna, malejąca częstość występowania znaczącej liczby na pierwszym miejscu w zbiorze została po raz pierwszy odnotowana w 1881 r. przez kanadyjskiego astronoma i matematyka Simona Newcomba. Przebywając w bibliotece, zauważył on, że strony tablic logarytmicznych są brudniejsze na początku i coraz czystsze na dalszych kartach.
Wywnioskował, że jest to spowodowane poszukiwaniem przez ich użytkowników niższych cyfr, znajdujących się na początku tablic.
To odkrycie nie spotkało się z szerszym zainteresowaniem. Dopiero w 1938 r. Frank Benford, inżynier General Electric, nieznający pracy Newcomba, dokonał tego samego odkrycia na podstawie stanu czystości tablic logarytmicznych.
[3] Zob. J. Szymanowski, Fenomen rozkładu Benforda, „Delta” nr 12/2010.
[4] Tamże.
Beford próbował sprawdzić, czy zjawisko to może dotyczyć również innych zbiorów danych, np. powierzchni rzek, liczb drukowanych w gazetach. Wyniki swoich badań przedstawił na łamach „Proceedings of the American Philosophical Society”, jednak formalny dowód nie został przedstawiony[3]. Pomimo to wiele przeprowadzonych eksperymentów dowodzi uniwersalności tego prawa – przykładowe potwierdzenie malejącej tendencji w częstości występowania cyfr można znaleźć w odniesieniu do powierzchni (w km2) wszystkich państw świata czy w masach atomowych pierwiastków w układzie okresowym[4].
Wstępna identyfikacja zniekształceń spowodowanych oszustwem
Prawo Benforda może posłużyć do wstępnej identyfikacji nieprawidłowości wywołanych oszustwem. Stosowane jest przykładowo do badania, czy występują nadużycia przy sprawdzaniu prawidłowości zeznań podatkowych.
[5] Tamże.
[6]Zob. J. Carlton Collins, Using Excel and Benford’s Law to detect fraud, „Journal of Accountancy” 2017, April.
Dokonujący fałszerstw starają się podawać liczby wyglądające na przypadkowe, zwykle jednak przeczące rozkładowi częstości Benforda. Okazuje się, że oszuści przeważnie wybierają liczby rozpoczynające się od 4, 5 i 6, a nie 1, 2 i 3. Za pomocą prawa pierwszych cyfr udało się m.in. wykryć fałszerstwo skarbnika stanu Arizona w USA, Jamesona Nelsona, na kwotę bliską 2 mln dolarów[5].
Wyjaśnieniem takiego sposobu postępowania może być ciekawy eksperyment przedstawiony przez J. Carltona Collinsa[6]. Celem eksperymentu było utworzenie przez grupę osób szeregu (1400) przypadkowych liczb na klawiaturze numerycznej komputera, przy czym cyfry od 1 do 9 na tej klawiaturze umieszczone były jak w większości laptopów, w układzie horyzontalnym.
Okazuje się, że cyfry 4, 5 i 6 były umieszczane na pierwszym miejscu znacznie częściej niż skrajne, czyli 1, 2 i 3 oraz 7, 8 i 9. Wyniki eksperymentu przedstawia poniższy rysunek.
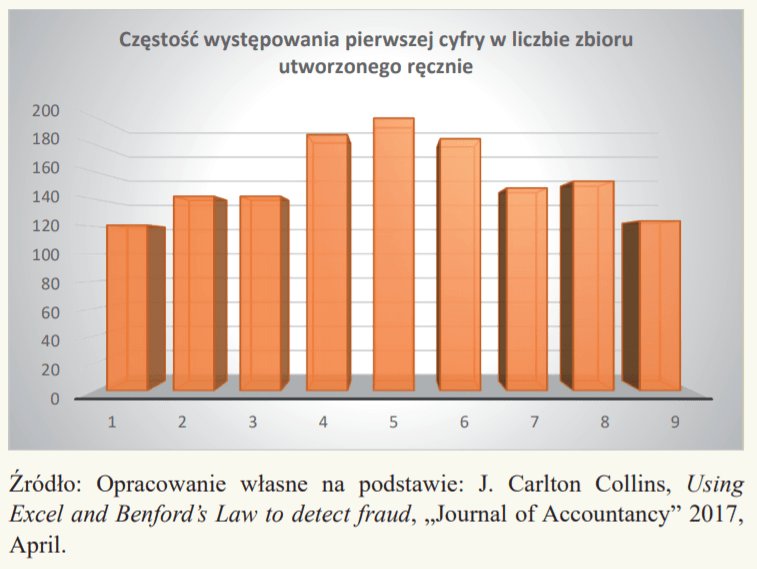
Wyniki są zgodne z rozsądnym założeniem, że częściej wybiera się cyfry umieszczone na klawiszach obsługiwanych przez palce środkowe i wskazujące dłoni niż skrajne.
Dla porównania na poniższym rysunku zaprezentowano rozkład częstości występowania pierwszej (znaczącej) cyfry w zbiorze 1090 liczb utworzonych przez komputer automatycznie, poza ingerencją człowieka.
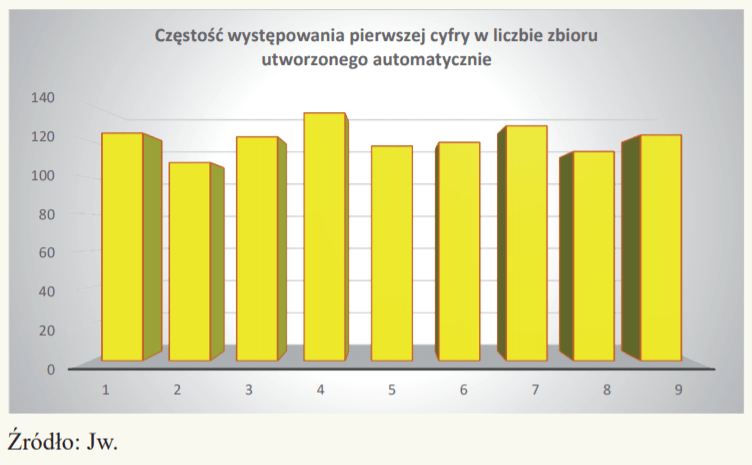
W przypadku liczb utworzonych automatycznie (losowo) przez komputer rozkład częstości pierwszej (znaczącej) cyfry w liczbie przyjmuje postać mniej więcej tak samo prawdopodobny dla każdej z cyfr – w prezentowanym przykładzie jedynie cyfry 1, 4, 7 i 9 zostały wybrane nieznacznie częściej niż pozostałe.
Przykład ten miał za zadanie przedstawić oraz w pewien sposób uzasadnić różnice między postępowaniem celowym (ludzkim) a uznanym za losowe (komputerowym). Można się pokusić o stwierdzenie, że prawo Benforda znajdowałoby się gdzieś pośrodku między tymi skrajnościami.
Warto też pamiętać, że prawo Benforda jest tylko jednym z narzędzi analitycznych wspierających pracę biegłego rewidenta, umożliwiającym identyfikację potencjalnych zniekształceń w zbiorze, mogących wskazywać na podwyższone ryzyko oszustwa. Bardziej rozbudowanym narzędziem jest przykładowo tzw. model Beneisha, który pomaga wykryć manipulacje wynikiem danej jednostki przy wykorzystaniu różnych wskaźników finansowych (rotacji należności, marży brutto, dynamiki sprzedaży itp.). Kwestia ta wykracza jednak poza ramy tego artykułu – skoncentrowano się w nim na prawie Benforda.
Stosowanie do badania prawa Benforda przy wykorzystaniu programu Excel
W opracowaniu przyjęto następującą konwencję prezentacji zagadnienia: w pierwszej kolejności zdefiniowanie problemu (określenie celu badania), w drugiej określenie sposobu jego rozwiązania przez wskazanie poszczególnych kroków, jakie należy wykonać, posługując się programem Excel.
Problem ogólny: Czy przychody nie są zniekształcane?
Problem: Czy zbiór obejmujący faktury sprzedaży może zawierać pozycje (faktury) noszące znamiona potencjalnych nadużyć (oszustw)?
Sposób rozwiązania: Ustalenie formuły pozwalającej na określenie liczby faktur o kwotach przychodu brutto (należności) rozpoczynających się cyfrą 1, 2, 3 itd. oraz porównanie uzyskanych wyników z rozkładem częstości Benforda.
Kroki postępowania:
[7] Na potrzeby prezentacji zagadnienia użyto fikcyjnej bazy danych.
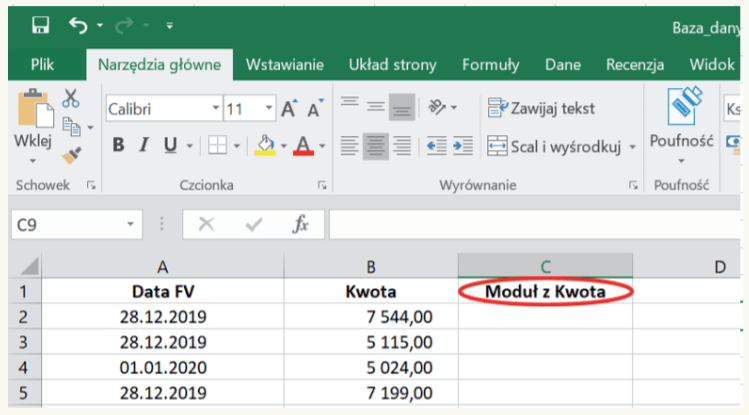
1. Podstawą badań jest wprowadzona do programu Excel baza danych w postaci poszczególnych faktur za badany rok, przy czym w przykładzie istotne są kwoty należności wykazane w fakturach[7] – zob. poniższy obraz przedstawiający fragment zbioru.
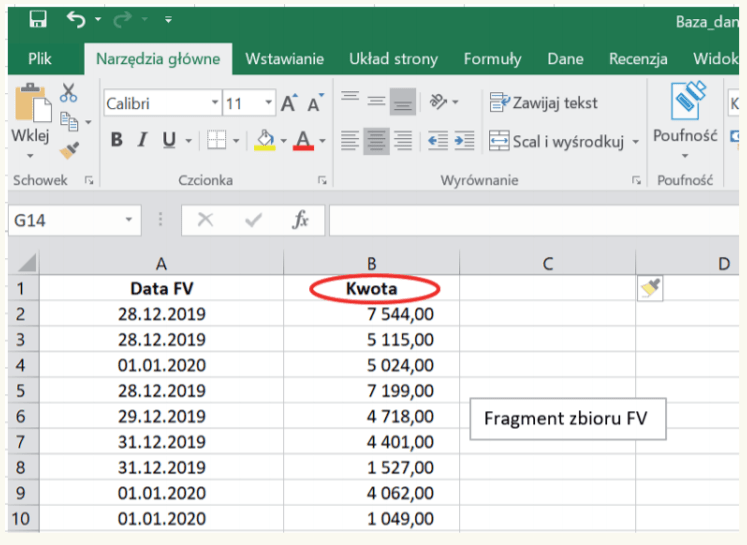
Zbiór faktur sprzedaży może zawierać faktury korygujące, co oznacza, że mogą się w nim pojawić zapisy ujemne. Dla ustalenia liczby faktur o wartościach rozpoczynających się określoną cyfrą (1, 2, 3 itd.) oraz porównania uzyskanych wyników z rozkładem częstości Benforda zbiór ten trzeba „oczyścić” z wartości ujemnych. W tym celu stosuje się zdefiniowaną w programie Excel funkcję: MODUŁ.LICZBY.
[8] Oczywiście nazwę tę biegły rewident może dobrać dowolnie, np. „Kwota bezwzględna faktury” albo „Kwota nieujemna faktury”.
Do komórki C1, tj. w kolumnie sąsiadującej z kolumną „Kwota”, wprowadzamy nazwę kolumny, która będzie zawierała pozbawione znaku „minus” kwoty faktur. Przykładowo może być to „Moduł z Kwota”[8] (zob. obraz poniżej).
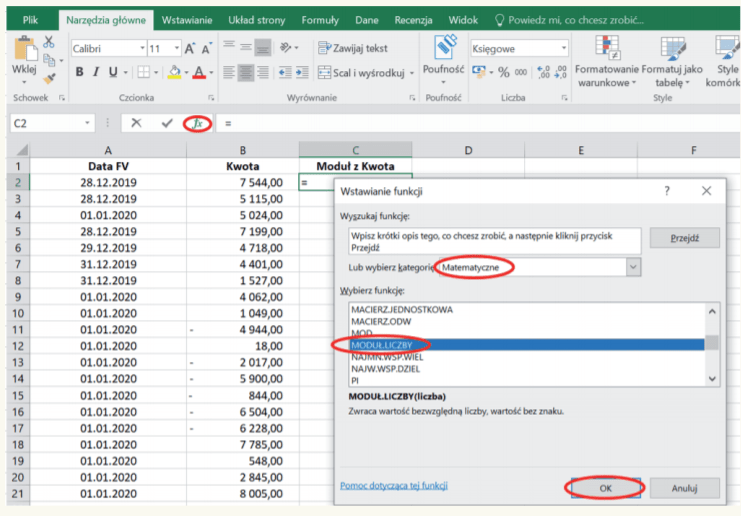
2. W pierwszej wolnej komórce, w kolumnie „Moduł z Kwota” (tu C2), klikamy symbol fx na pasku zadań; w rozwijanym oknie wyboru „Wybierz kategorię” wybieramy kategorię „Matematyczne”, a w jej ramach odnajdujemy wskazaną funkcję: MODUŁ.LICZBY, i zatwierdzamy „OK”. Ilustruje to poniższy obraz.
3. W okienku „Argumenty funkcji” wpisujemy B2, gdyż chcemy, aby program zamieniał ew. ujemne wartości faktur na dodatnie począwszy od pierwszej pozycji w zbiorze (zob. obraz poniżej).
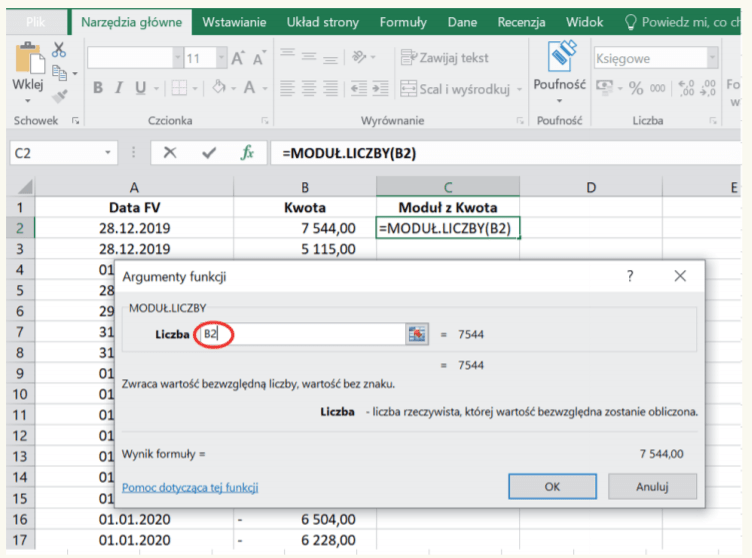
4. Po kliknięciu „OK” program wyświetla wyliczoną przez funkcję wartość (tu w komórce C2); będzie to wartość analogiczna do wykazanej w komórce B2, gdyż jest to wartość dodatnia.
5. Wprowadzoną do komórki C2 formułę kopiujemy „w dół” w ramach kolumny „Moduł z Kwota”, tak aby objąć nią cały zbiór faktur (tu 10 115 pozycji). Szybki sposób kopiowania formuły do komórek przedstawiono w kolejnych krokach.
6. Utworzoną w komórce C2 formułę – na powyższym obrazie to formuła „=MODUŁ.LICZBY(B2)” – kopiujemy (Ctrl + C), zaznaczamy kursorem wszystkie pozostałe komórki w kolumnie: „Moduł z Kwota” (tj. komórki C3 i dalej aż do końca zbioru) i wklejamy (Ctrl + V).
Dla przypomnienia: w tym przypadku korzystamy w formule z tzw. adresowania względnego, co oznacza, że nie blokujemy ani kolumn, ani wierszy. Jest to zgodne z naszym zamiarem, gdyż chcemy, aby program stosował formułę krok po kroku (tj. komórka po komórce). Gdyby zastosowano blokadę np. wiersza 2 kolumny B – zapis formuły: MODUŁ.LICZBY(B$2) – program każdorazowo odnosiłby się do tej właśnie komórki w zablokowanym wierszu 2.
7. Aby szybko zaznaczyć wszystkie komórki (tu 10 115) w kolumnie „Moduł z Kwota” i wkleić do nich skopiowaną uprzednio formułę – zaznaczamy komórkę w kolumnie obok, zawierającą dane (tu „Kwota”) i stosujemy skrót klawiaturowy Ctrl + strzałka w dół. W ten sposób przechodzimy do ostatniego wiersza danych tej kolumny.
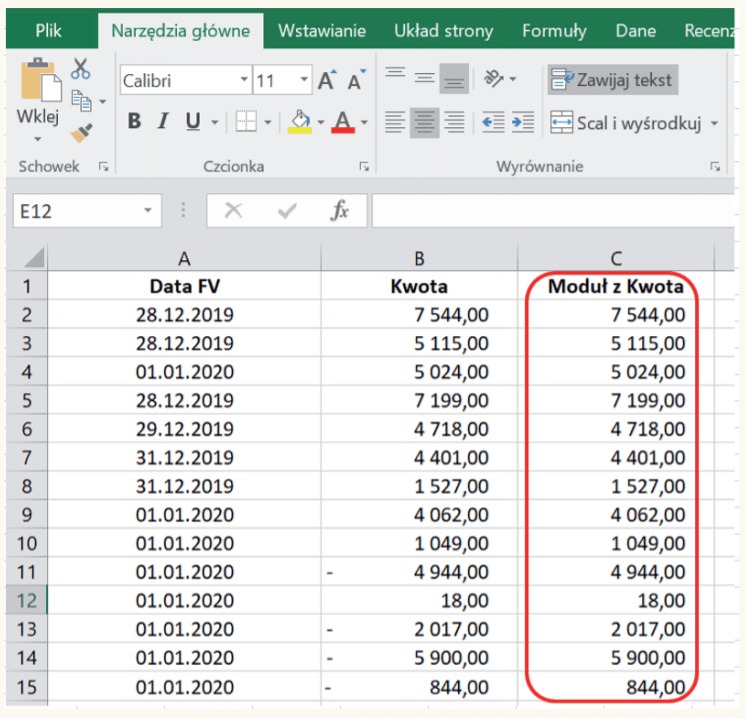
Przy ostatnim wierszu danych przechodzimy do ostatniej komórki w kolumnie „Moduł z Kwota” i stosujemy skrót Ctrl + strzałka w górę. Po naciśnięciu „Enter” skopiowana uprzednio formuła zostanie automatycznie włączona (wklejona) do wszystkich komórek. W ten sposób otrzymujemy 10 115 pozycji wypełnionych nieujemnymi wartościami faktur (zob. obraz poniżej).
[9] LEWY, gdyż rozpoczyna analizę wprowadzonych w komórkach wartości od lewej strony.
8. Aby program mógł obliczyć, ile kwot faktur zaczynało się od cyfr 1, 2, 3 itd., do kolejnej kolumny wprowadza się odpowiednią formułę, która pozwala na wyłonienie tych cyfr z wartości faktur. W programie Excel formuła ta nazywa się LEWY[9]. Jej budowa jest następująca:
LEWY(Tekst; Liczba znaków),
gdzie:
Tekst – ciąg tekstowy (liczbowy) zawierający znaki do wyodrębnienia,
Liczba znaków – ile znaków ma zostać wyodrębnionych przez funkcję LEWY.
9. Załóżmy, że program będzie dokonywał wyliczeń w kolumnie, którą nazwiemy „Pierwsza cyfra” – zob. poniższy obraz.
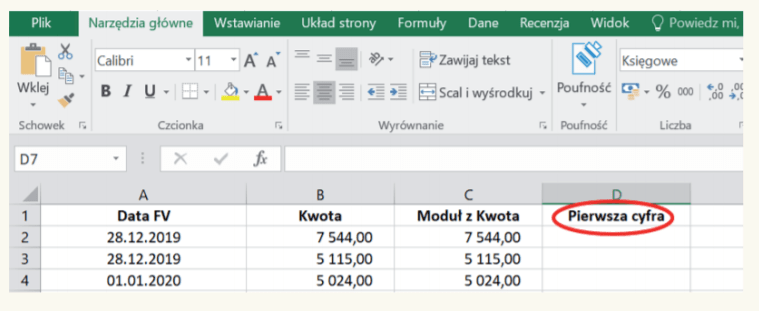
10. Do pierwszej komórki kolumny D, tj. komórki D2, wprowadzamy formułę LEWY. W tym celu, podobnie jak przy formule MODUŁ.LICZBY, klikamy symbol fx na pasku zadań; w rozwijanym oknie wyboru „wybierz kategorię” wybieramy kategorię „Tekstowe”, a w jej ramach funkcję LEWY, i zatwierdzamy „OK”. Ilustruje to poniższy obraz.
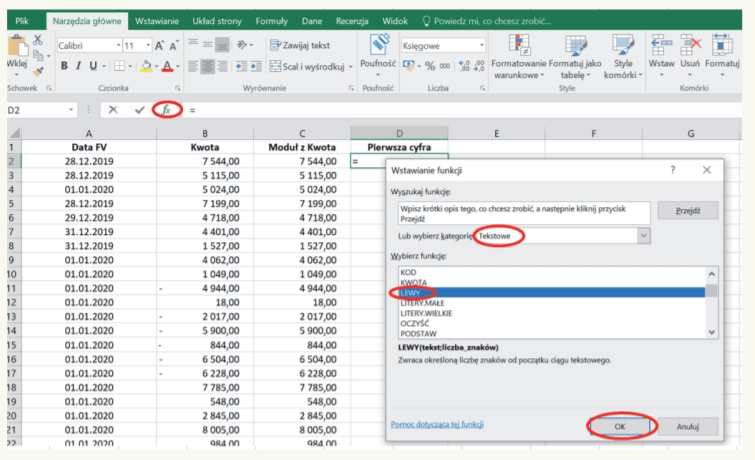
11. W okienku „Argumenty funkcji”, w polu „Tekst” wpisujemy C2, gdyż chcemy, aby program analizował wartości począwszy od tej właśnie komórki. W polu „Liczba znaków” wpisujemy 1, gdyż chcemy, aby program wyodrębniał pierwszą cyfrę od lewej strony (zob. obraz poniżej).
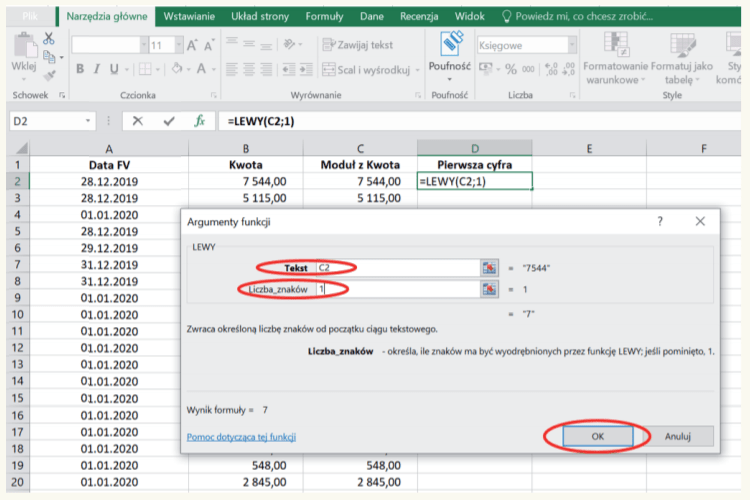
12. Po kliknięciu „OK” program wyświetla wynik zastosowanej funkcji (tu cyfrę 7) jako pierwszą od lewej, w kwocie 7544,00.
13. Formułę LEWY wprowadzamy do pozostałych komórek w ramach kolumny „Pierwsza cyfra”. Postępujemy analogicznie jak w pkt 5–7.
14. W wyniku przeprowadzonych działań w kolumnie z danymi (kolumna „Pierwsza cyfra”) otrzymujemy dane wymagające analizy (zliczenia) na potrzeby porównań z rozkładem Benforda.
15. Aby ustalić, ile faktur wykazuje kwotę przychodu brutto rozpoczętą (pierwszą) cyfrą 1, 2, 3... 9, kolejne 3 kolumny nazwiemy odpowiednio: „Statystyka zbioru – pierwsza cyfra”, „Częstość”, „% dowodów w ogóle” – zob. poniższy obraz.
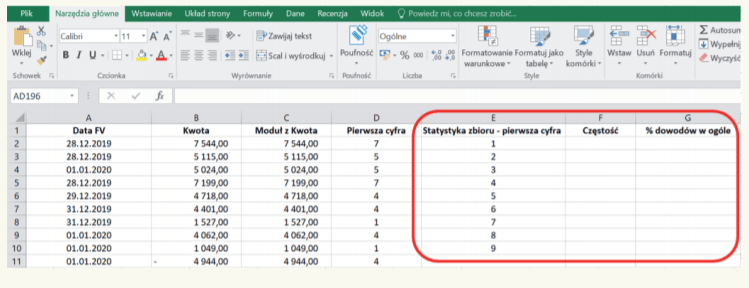
16. Kolumna E „Statystyka zbioru – pierwsza cyfra” zawiera możliwe pierwsze cyfry początkowe kwoty faktur. W kolumnie F „Częstość” wprowadzamy kolejną formułę, która automatycznie zbada zbiór danych w kolumnie „Pierwsza cyfra”, tj. zliczy, ile razy wystąpiła cyfra 1, ile razy cyfra 2 itd. aż do 9. Formuła ta nazywa się w programie Excel: LICZ.JEŻELI, i jest dostępna w kategorii funkcji „Statystyczne”. Funkcja ta ma następującą budowę:
LICZ.JEŻELI(Zakres; Kryteria),
gdzie:
Zakres – zakres komórek, w którym będą zliczane komórki, które nie są puste,
Kryteria – kryteria podane w formacie liczby, wyrażenia lub tekstu, które będą uwzględniane przy zliczaniu.
17. W pierwszej komórce kolumny F („Częstość”), tj. komórce F2, wprowadzamy formułę LICZ.JEŻELI. W tym celu, podobnie jak poprzednio, klikamy symbol fx na pasku zadań, w rozwijanym oknie wyboru „wybierz kategorię” wybieramy kategorię „Statystyczne”, a w jej ramach wskazaną funkcję LICZ.JEŻELI, i zatwierdzamy „OK”. Przedstawia to poniższy obraz.
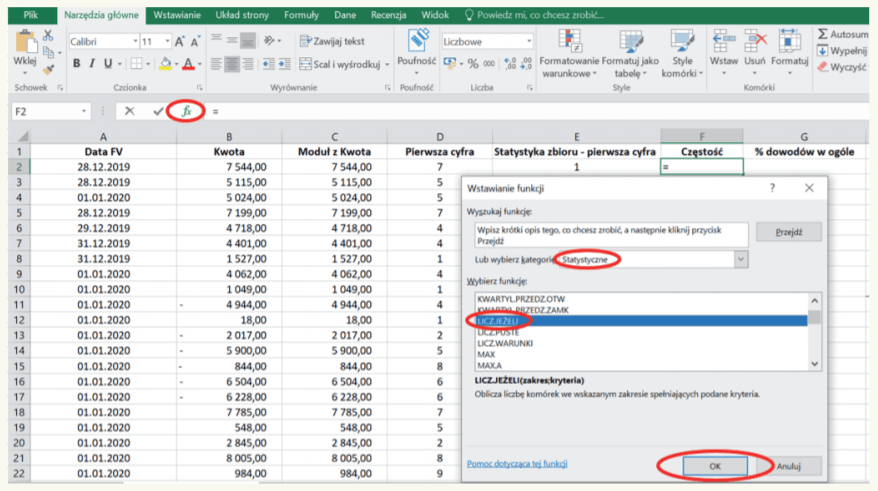
[10] W związku z tym, że baza będzie wykorzystywana do badania występowania również pozostałych cyfr, tj. 2, 3… 9, wprowadzamy blokadę jej adresu przez wpisanie, przed literą i liczbą, symbolu dolara (skrót Shift + 4), czyli $D$2:$D$10116. W wyniku tego zabiegu przy kopiowaniu formuły do pozostałych komórek adres ten nie będzie ulegał zmianie mimo zmiany komórki, do której formuła będzie kopiowana.
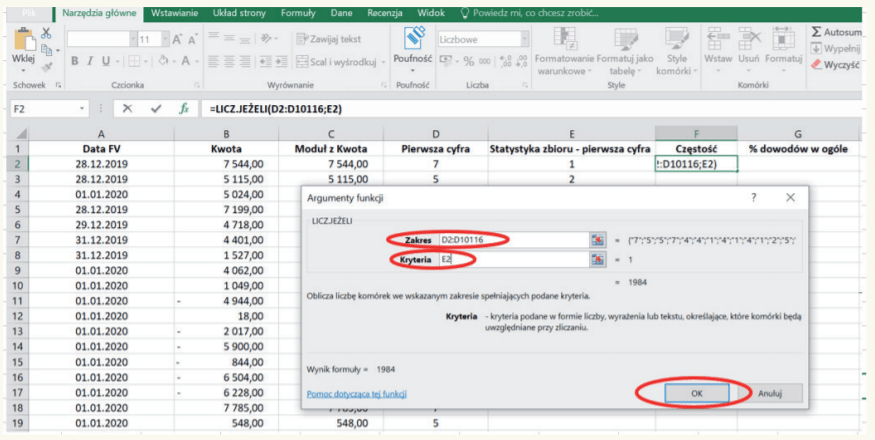
18. W okienku „Argumenty funkcji” w polu „Zakres” wpisujemy $D$2:$D$10116, gdyż chcemy, aby program zbadał całą bazę wartości od komórki D2 do D10116[10]; w okienku „Kryteria” wpisujemy E2, gdyż chcemy, aby program za kryterium badania obrał cyfrę podaną przez nas w tej komórce (zob. obraz poniżej).
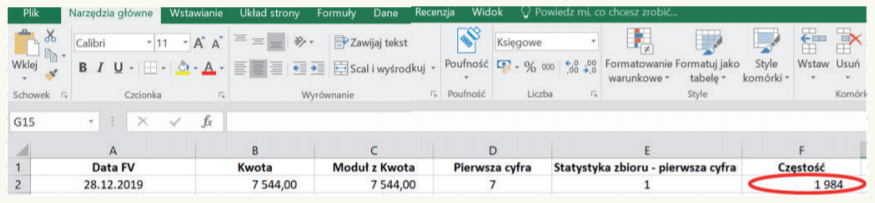
Po kliknięciu „OK” w komórce F2 otrzymujemy wynik 1984. Oznacza to, że w badanym zbiorze występują 1984 faktury, których wartość rozpoczyna się od cyfry 1 – zob. poniższy obraz).
19. Formułę wprowadzoną do komórki F2 kopiujemy do pozostałych komórek, tj. od F3 do F10. Wykorzystujemy sposób kopiowania opisany w pkt 5–7. Warto zaznaczyć, że dzięki zablokowaniu zakresu danych za pomocą znaku $, przy kopiowaniu formuły do kolejnych komórek F3–F10 zakres ten nie ulegnie zmianie. Zmieniać się będzie tylko komórka z kryterium, np. w komórce F10 w formule po średniku pojawi się E10. W komórce F10 formuła będzie wyglądała następująco: =LICZ.JEŻELI($D$2:$D$10116;E10).
20. Pozostaje obliczyć procent wyliczonej przez program częstości faktur, których wartość rozpoczyna się od cyfry 1, 2, 3… 9, w ogólnej liczbie faktur. Można to oczywiście przeliczyć na kalkulatorze, jednak znacznie szybciej zrobi to program.
21. W kolumnie G „% dowodów w ogóle” do komórki G2 wprowadzamy formułę: =F2/SUMA($F$2:$F$10). Podobnie jak poprzednio trzeba zablokować zbiór, do którego program będzie się każdorazowo odnosił w obliczeniach (tu suma wszystkich wyliczonych w kolumnie F częstości). Licznik pozostaje bez blokady, gdyż przy kopiowaniu formuły do kolejnych komórek program każdorazowo będzie „przesuwał się” o jedną komórkę. W ostatniej komórce (G10) formuła będzie następująca: =F10/SUMA($F$2:$F$10).
22.W wyniku przeprowadzonych czynności otrzymamy zestawienie pokazujące rozkład częstości występowania w wartościach faktur na pierwszym miejscu cyfry 1, 2, 3… 9. W omawianym przykładzie zestawienie takie przedstawia tabela.
Rozkład Benforda wskazuje prawidłowość, zgodnie z którą częstość występowania na pierwszym miejscu w rzeczywistych danych kolejnych cyfr znacząco maleje (począwszy od 30,1% dla cyfry 1, a kończąc na 4,6% dla cyfry 9). Przeprowadzone badanie zbioru faktur wykazuje, że jego dane nie są w pełni zgodne z rozkładem Benforda. W szczególności można zaobserwować istotną różnicę w częstości występowania faktur o wartościach rozpoczynających się od cyfr 1, 4 i 5.
| Statystyka zbioru – pierwsza cyfra | Częstość występowania | ||
| badany zbiór faktur (liczba przypadków) | badany zbiór faktur (w % ogółu) | rozkład Benforda (wartość referencyjna mw % ogółu) | |
| 1 | 1 984 | 19,6 | 30,1 |
| 2 | 1 379 | 13,6 | 17,6 |
| 3 | 682 | 6,8 | 12,5 |
| 4 | 2 197 | 21,7 | 9,7 |
| 5 | 1 340 | 13,3 | 7,9 |
| 6 | 730 | 7,2 | 6,7 |
| 7 | 942 | 9,3 | 5,8 |
| 8 | 503 | 5,0 | 5,1 |
| 9 | 358 | 3,5 | 4,6 |
| 10 115 | 100 | 100 | |
Wyniki mogą być także przedstawione na wykresie.
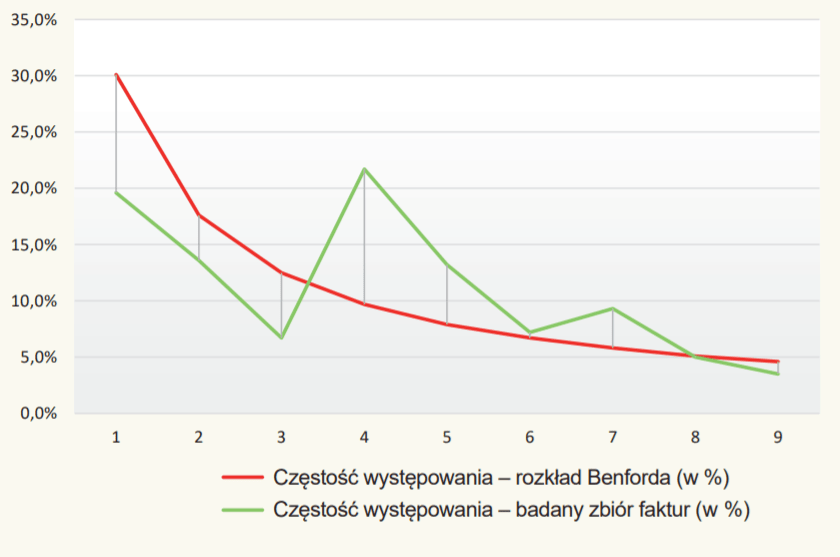
Wynik badania, bez względu na postać prezentacji (tabela, wykres) wskazuje na występowanie znacznych odchyleń od wzorca, co może sygnalizować potencjalne nadużycia (oszustwa). Dlatego biegły rewident może na jego podstawie dojść do wniosku, że w ramach dalszych prac (np. badania wiarygodności) zasadne jest zbadać zbiór faktur, w odniesieniu do których odnotowano największą rozbieżność w stosunku do rozkładu Benforda (tu faktury o wartościach rozpoczynających się od cyfry 4).
W przykładzie posłużono się zbiorem faktur sprzedażowych, analizując możliwość potencjalnego zniekształcenia przychodów. Prawo Benforda może być również użyteczne do analizy innych danych księgowych, np. transakcyjnych (wydatki, wypłaty). Każdorazowo jednak uwzględnienia wymagają ograniczenia jego stosowania.
Ograniczenia stosowania prawa Benforda
Stosując prawo Benforda, należy pamiętać o jego ograniczeniach. W szczególności o przypadkach, w których rozkład ten nie będzie miał zastosowania. Przykładowo badany zbiór danych może zawierać jedynie wartości rozpoczynające się od cyfr większych od 3 – gdyż np. jednostka oferuje swoje produkty w cenach od 400 do 950 zł.
[11] Zob. J. Krawiec, Prawo Benforda jako narzędzie wykrywania manipulacji finansowych, „Kwartalnik Nauk o Przedsiębiorstwie” nr 4/2012.
Innym ograniczeniem może być mała liczebność zbioru – rozkład Benforda bazuje na dużych zbiorach danych; zwykle przyjmuje się, że powinny one obejmować więcej niż 1000 pozycji[11].
Nie istnieją także jednoznaczne reguły określające, jakiego rzędu odchylenia częstości występowania znaczących cyfr w analizowanym zbiorze od tych w rozkładzie Benforda można uznać za prawidłowe, a które powinny zostać poddane dalszym analizom. Zwykle przedmiotem kolejnych badań są dowody wykazujące największe odchylenia.
Prawo Benforda może pomóc we wstępnej identyfikacji potencjalnych nieprawidłowości, w tym spowodowanych oszustwem. Nie jest to jednak jedyne narzędzie. Racjonalne jest stosowanie przez biegłego rewidenta również innych procedur analitycznych w celu rozpoznania nietypowych lub nieoczekiwanych powiązań i trendów.
Wszelkie narzędzia analityczne jedynie wspomagają i uzupełniają zawodowy sceptycyzm oraz osąd biegłego rewidenta.
Zaloguj się
Aby czytać dalej, jeśli masz wykupiony abonament
Kup dostęp do tego artykułu
Cena dostępu do pojedynczego artykułu tylko 12,30
Kup abonament
| Abonamenty on-line | Prenumeratorzy | Członkowie SKwP | ||||||||
|
Bezpłatny dostęp do tego artykułu i ponad 3500 innych, dla prenumeratorów miesięcznika „Rachunkowość". Pomoc w uzyskaniu dostępu:
|
15% rabat na wszystkie zakupy. Zapytaj o kod w swoim Oddziale. Stowarzyszenie Księgowych w Polsce jest organizacją, do której należy ponad 26 000 księgowych, a członkostwo wiąże się z licznymi korzyściami. |
„Rachunkowość” - od 75 lat źródło rzetelnej wiedzy!
Skróty w artykułach
- dyrektywa 112 – dyrektywa Rady 2006/112/WE z 28.11.2006 r. w sprawie wspólnego systemu podatku od wartości dodanej (DzUrz UE L 347 z 11.12.2006 r.)
- dyrektywa 2013/34/UE – dyrektywa Parlamentu Europejskiego i Rady 2013/34/UE z 26.06.2013 r. w sprawie rocznych sprawozdań finansowych, skonsolidowanych sprawozdań finansowych i powiązanych sprawozdań niektórych rodzajów jednostek (...) (DzUrz UE L 182 z 29.06.2013 r.)
- Kc – ustawa z 23.04.1964 r. Kodeks cywilny (DzU z 2023 r. poz. 1610)
- KIMSF – interpretacje Komitetu ds. Interpretacji Międzynarodowej Sprawozdawczości Finansowej
- Kks – ustawa z 10.09.1999 r. Kodeks karny skarbowy (DzU z 2023 r. poz. 654)
- Kp – ustawa z 26.06.1974 r. Kodeks pracy (DzU z 2023 r. poz. 1465)
- Kpc – ustawa z 17.11.1964 r. Kodeks postępowania cywilnego (DzU z 2023 r. poz. 1550)
- Ksh – ustawa z 15.09.2000 r. Kodeks spółek handlowych (DzU z 2022 r. poz. 1467)
- KSR – Krajowe Standardy Rachunkowości
- MSR – Międzynarodowe Standardy Rachunkowości (ang. International Accounting Standards) wydawane od 2002 r. jako MSSF
- MSSF – Międzynarodowe Standardy Sprawozdawczości Finansowej (ang. International Financial Reporting Standards)
- Op – ustawa z 29.08.1997 r. Ordynacja podatkowa (DzU z 2023 r. poz. 2383)
- Ppsa – ustawa z 30.08.2002 r. Prawo o postępowaniu przed sądami administracyjnymi (DzU z 2023 r. poz. 1634)
- rozporządzenie o instrumentach finansowych – rozporządzenie Ministra Finansów z 12.12.2001 r. w sprawie szczegółowych zasad uznawania, metod wyceny, zakresu ujawniania i sposobu prezentacji instrumentów finansowych (DzU z 2017 r. poz. 277)
- rozporządzenie o konsolidacji – rozporządzenie Ministra Finansów z 25.09.2009 r. w sprawie szczegółowych zasad sporządzania przez jednostki inne niż banki, zakłady ubezpieczeń i zakłady reasekuracji skonsolidowanych sprawozdań finansowych grup kapitałowych (DzU z 2017 r. poz. 676)
- rozporządzenie składkowe – rozporządzenie Ministra Pracy i Polityki Socjalnej z 18.12.1998 r. w sprawie szczegółowych zasad ustalania podstawy wymiaru składek na ubezpieczenia emerytalne i rentowe (DzU z 2023 r. poz. 728)
- rozporządzenie z 13.09.2017 r. – rozporządzenie Ministra Rozwoju i Finansów w sprawie rachunkowości oraz planów kont dla budżetu państwa, budżetów jednostek samorządu terytorialnego, jednostek budżetowych, samorządowych zakładów budżetowych, państwowych funduszy celowych oraz państwowych jednostek budżetowych mających siedzibę poza granicami Rzeczypospolitej Polskiej (DzU z 2020 r. poz. 342)
- specustawa – ustawa z 2.03.2020 r. o szczególnych rozwiązaniach związanych z zapobieganiem, przeciwdziałaniem i zwalczaniem COVID-19, innych chorób zakaźnych oraz wywołanych nimi sytuacji kryzysowych (tekst jedn. DzU z 2023 r. poz. 1327)
- uobr – ustawa z 11.05.2017 r. o biegłych rewidentach, firmach audytorskich oraz nadzorze publicznym (DzU z 2023 r. poz. 1015)
- uor – ustawa z 29.09.1994 r. o rachunkowości (DzU z 2023 r. poz. 120)
- updof – ustawa z 26.07.1991 r. o podatku dochodowym od osób fizycznych (DzU z 2022 r. poz. 2647)
- updop – ustawa z 15.02.1992 r. o podatku dochodowym od osób prawnych (DzU z 2022 r. poz. 2587)
- upol – ustawa z 12.01.1991 r. o podatkach i opłatach lokalnych (DzU z 2023 r. poz. 70)
- US GAAP – Amerykańskie Standardy Rachunkowości (ang. Generally Accepted Accounting Principles)
- ustawa akcyzowa – ustawa z 6.12.2008 r. o podatku akcyzowym (DzU z 2023 r. poz. 1542)
- ustawa emerytalna – ustawa z 17.12.1998 r. o emeryturach i rentach z Funduszu Ubezpieczeń Społecznych (DzU z 2023 r. poz. 1251)
- ustawa KAS – ustawa z 16.11.2016 r. o Krajowej Administracji Skarbowej (DzU z 2023 r. poz. 615)
- ustawa o KRS – ustawa z 20.08.1997 r. o Krajowym Rejestrze Sądowym (DzU z 2023 r. poz. 685)
- ustawa o PCC – ustawa z 9.09.2000 r. o podatku od czynności cywilnoprawnych (DzU z z 2023 r. poz. 170)
- ustawa o VAT – ustawa z 11.03.2004 r. o podatku od towarów i usług (DzU z 2023 r. poz. 1570)
- ustawa o zfśs – ustawa z 4.03.1994 r. o zakładowym funduszu świadczeń socjalnych (DzU z 2023 r. poz. 998)
- ustawa zasiłkowa – ustawa z 25.06.1999 r. o świadczeniach pieniężnych z ubezpieczenia społecznego w razie choroby i macierzyństwa (DzU z 2022 r. poz. 1732)
- ustawa zdrowotna – ustawa z 27.08.2004 r. o świadczeniach opieki zdrowotnej finansowanych ze środków publicznych (DzU z 2022 r. poz. 2561)
- usus – ustawa z 13.10.1998 r. o systemie ubezpieczeń społecznych (DzU z 2023 r. poz. 1230)
- uzpd – ustawa o zryczałtowanym podatku dochodowym od niektórych przychodów osiąganych przez osoby fizyczne
- Założenia koncepcyjne MSSF – Założenia koncepcyjne sprawozdawczości finansowej (Conceptual Framework for Financial Reporting)
- CEIDG – Centralna Ewidencja i Informacja o Działalności Gospodarczej
- EOG – Europejski Obszar Gospodarczy
- FEP – Fundusz Emerytur Pomostowych
- FGŚP – Fundusz Gwarantowanych Świadczeń Pracowniczych
- FP – Fundusz Pracy
- FS – Fundusz Solidarnościowy
- IASB – Rada Międzynarodowych Standardów Rachunkowości
- IS – izba skarbowa
- KAS – Krajowa Administracja Skarbowa
- KIS – Krajowa Informacja Skarbowa
- KNF – Komisja Nadzoru Finansowego
- KRBR – Krajowa Rada Biegłych Rewidentów
- KRS – Krajowy Rejestr Sądowy
- KSB – Krajowe Standardy Badania
- MF – Minister Finansów
- MPiPS – Minister Pracy i Polityki Społecznej
- MRiF – Minister Rozwoju i Finansów
- MRiPS – Minister Rodziny i Polityki Społecznej
- MSiG – Monitor Sądowy i Gospodarczy
- NSA – Naczelny Sąd Administracyjny
- PANA – Polska Agencja Nadzoru Audytowego
- PIBR – Polska Izba Biegłych Rewidentów
- PKD – Polska Klasyfikacja Działalności
- pkpir – podatkowa księga przychodów i rozchodów
- PPK – pracownicze plany kapitałowe
- RM – Rada Ministrów
- SA – sąd apelacyjny
- sf – sprawozdanie finansowe
- skok – spółdzielcza kasa oszczędnościowo-kredytowa
- SN – Sąd Najwyższy
- SO – sąd okręgowy
- TK – Trybunał Konstytucyjny
- TSUE – Trybunał Sprawiedliwości Unii Europejskiej
- UCS – urząd celno-skarbowy
- UE – Unia Europejska
- US – urząd skarbowy
- WDT – wewnątrzwspólnotowa dostawa towarów
- WNT – wewnątrzwspólnotowe nabycie towarów
- WSA – wojewódzki sąd administracyjny
- zfśs – zakładowy fundusz świadczeń socjalnych








